进城务工人员小梅之前看了书一直没有总结，现在开始结合之前学习的内容和正式的学习，对几本书及其他的一些资料进行总结，可以通过感性+公式来快速建立对深度学习基础知识的理解。
一、人工智能、机器学习、深度学习的关系
1956年的“达特茅斯夏季人工智能研讨会（Summer Research Project on Artificial Intelligence）”被广泛认为是现代人工智能研究的诞生之日，这次会议的议题覆盖了包括神经网络、自然语言处理、机器智能等人工智能的各个领域。人工智能是一个跨学科的领域，覆盖了计算机科学、数学、神经科学、心理学、哲学等领域的知识。按其针对领域的泛化程度可分为通用人工智能（General Artificial Intelligence）/强人工智能和狭义人工智能（Narrow Artificial Intelligence）或弱人工智能，其中：
· 通用人工智能即试图让机器拥有人类所有的感觉、理智，像人类一样思考，这到目前为止还显然是不可能的；
· 狭义人工智能则是希望让机器在某些领域表现得与人类一样好甚至更好，这些领域可能包括模式识别、机器视觉（物体识别、光学字符识别等）、语音识别、自然语言处理、人机博弈等；
人工智能、机器学习、深度学习之间的关系是递进的包含关系，即人工智能>机器学习>深度学习：
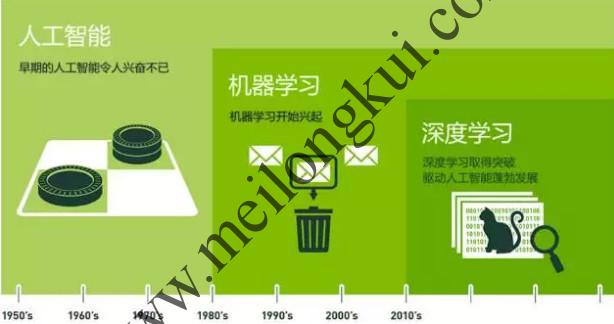
人工智能、机器学习、深度学习的关系
在信息革命后，随着计算机计算能力的增强，机器正在逐渐替代人，参与到更多“带有一定智能性”的信息分拣与识别工作中，即概念上的分类（classification）与回归（regression）问题。传统意义上的“算法”是让计算机按照固定的指令序列对输入数据进行处理，没有任何“学习”行为；而机器学习则是一种让计算机利用数据，而不是根据为解决特定任务、硬编码的指令，来进行工作的方法，其基本思想是基于数据构建统计模型并利用模型对数据进行分析和预测。机器学习的本质性目在于让机器帮助人类做一些大规模的数据识别、分拣、规律总结等人类做起来比较花时间的事情，是一门数据驱动的科学。
按照机器学习到层次特征的深度，可以将机器学习分为浅层学习和深度学习，其中：
· 浅层学习即传统的统计机器学习，主要基于概率统计原理，包括KNN（K-Nearest Neighbor，K近邻）、决策树、SVM（Support Vector Machine，支持向量机）、朴素贝叶斯等，在诸如垃圾邮件处理等方面发挥了重要的作用。这些传统机器学习算法大部分靠线性模型或者统计学概率模型能够给出清晰的物理含义解释，例如贝叶斯就是使用统计的方法解释不同时间先验概率和后验概率的量化关系计算问题，决策树是信息熵的降低问题，SVM是寻找超平面（后详）。传统机器算法需要人工提取特征，然后让模型进行权重学习；然而，在很多问题上通过人工方式设计有效的特征集合是困难甚至不可能。由于传统机器学习的大多数算法都是浅层学习，无法有效学习到数据的深层次特征，因此使得人工智能没有办法取得进一步的突破。深度学习的出现和发展逐步打破了这种现状，使得弱人工智能的任务在能力上较传统机器学习算法有了进一步的提升，也更让人们看到了实现通用人工智能的可能。
· 深度学习（Deep Learning，DL）解决的核心问题之一就是实现机器自动地抽取客观实体的特征，并自动地将简单的特征组合成更加复杂的特征，并使用这些组合特征解决问题。深度学习算法可以从数据中学习更加复杂的特征表达，使得权重学习变得更加简单和有效。深度学习所得出的模型往往是人类无法直观理解的黑盒子。
浅层学习与深度学习
按照机器学习实现目标的不同，可以将机器学习分为监督学习（Supervised learning）、无监督学习（Unsupervised learning）和强化学习（Reinforcement learning），其中：
· 监督学习，使用带有标签的训练数据集进行训练，输入的训练数据由客观实体的特征向量（输入）和客观实体的标签（输出）两部分构成，若输出的标签是一个连续的值则称为回归监督学习，若输出标签是一个离散的值则称为分类监督学习。KNN、SVM、决策树、Logistic回归都是常见监督学习算法。
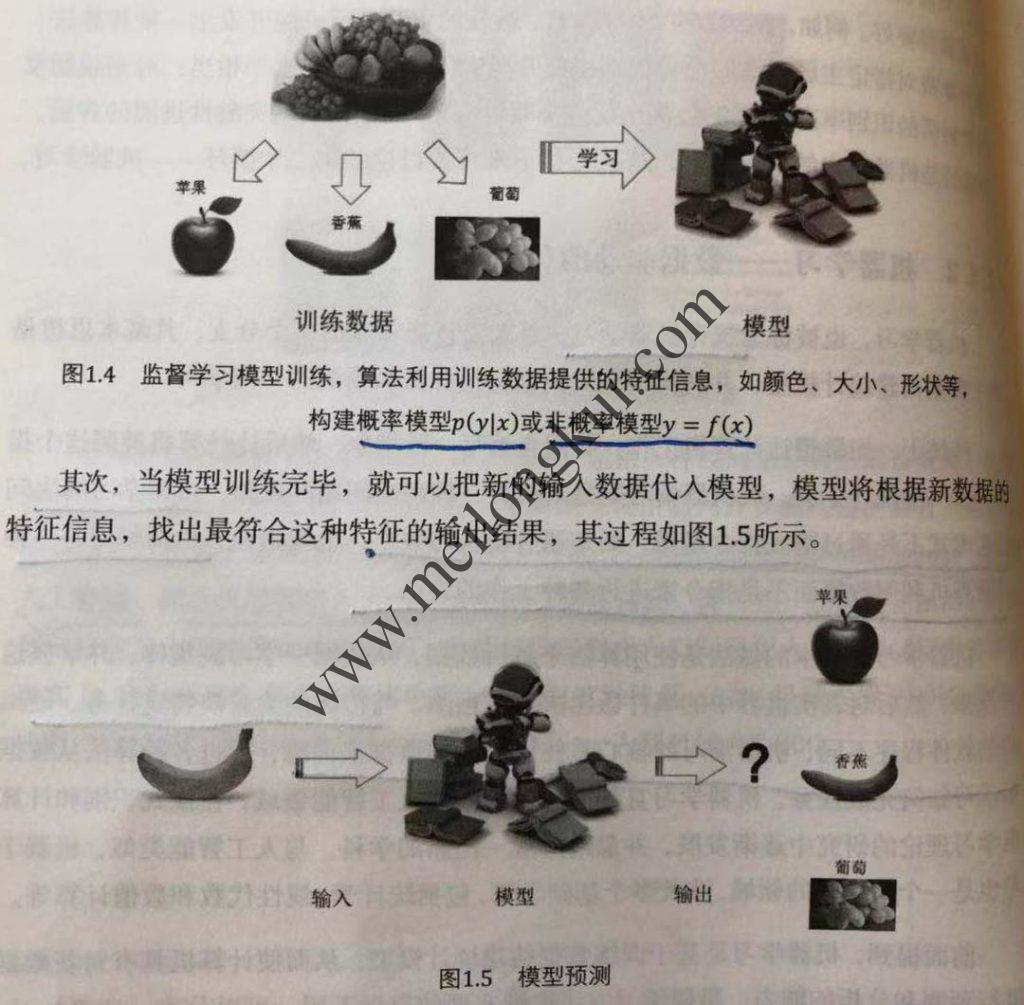
监督学习
· 无监督学习，训练样本数据没有任何标签和输出，其目的是对原始数据结构进行深入分析，找出数据间存在的规律与关系，包括数据聚类、数据降维和特征提取等。虽然监督学习的准确率更高，但是在现实生活中，我们获取的大量数据一般是没有标签数据的，因此我们不得不诉诸于无监督学习。传统的无监督学习方法在特征提取上并不令人满意，而深度学习则被证明具有强大的无监督学习能力，特别是在计算机视觉领域，运用深度学习技术所达到的效果更是要远优于传统的机器学习。
· 强化学习，也称为增强学习，强调如何基于环境而行动以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论，即有机体如何在环境给予的奖励和惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的习惯性行为。强化学习与监督学习和无监督学习之间的区别在于并不需要出现正确的输入输出对，也不需要精确校正次优化的行为。强化学习更加关注于在线规划，需要在探索未知的领域和遵从现有的知识之间找到平衡，其学习过程是一个从实际环境中不断学习、积累、不断进化的过程。因此，强化学习更接近于生物学习的本质，也是有期望让机器获得通用智能的一项技术。
二、线性不可分问题
在分类问题中，最简单的分类就是二分类问题，而且这个二分类问题是一个线性可分问题。所谓线性可分（linearly separable），简单地说就是能够用一个线性函数（形如f(x)=wx+b的线性分类器）将两类样本完全分开，同时称这些样本是“线性可分”的。
在一维空间，也就是一个坐标轴上面，要分开两个可以分开的点集合，我们只需要找到一个点：
一维线性可分示意图
在二维空间中，要分开两个线性可分的点集合，我们需要找到一条分类直线：
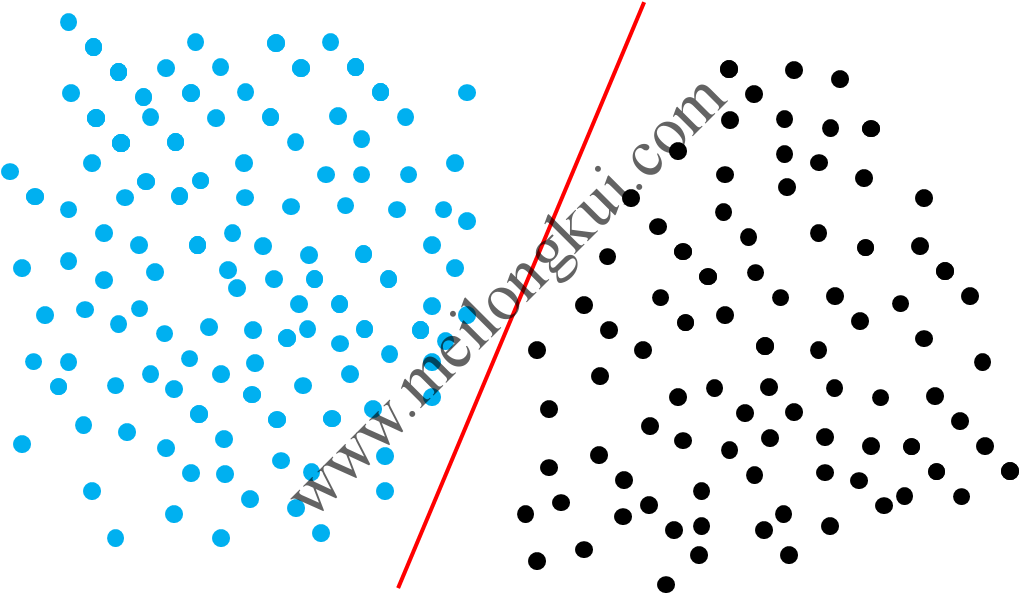
二维线性可分示意图
在三维空间中，要分开两个线性可分的点集合，我们需要找到一个平面：
三维线性可分示意图
在无法直接画出的在n维空间中，要分开两个线性可分的点集合，则需要找到一个超平面（Hyper Plane）。
我们可以很容易地找到线性不可分的情况，以二维空间为例，假设二维平面x-y上存在若干点，其中点集A服从{x,y|x^2+y^2=1}，点集B服从{x,y|x^2+y^2=9}，那么这些点在二维平面上的分布是这样的：
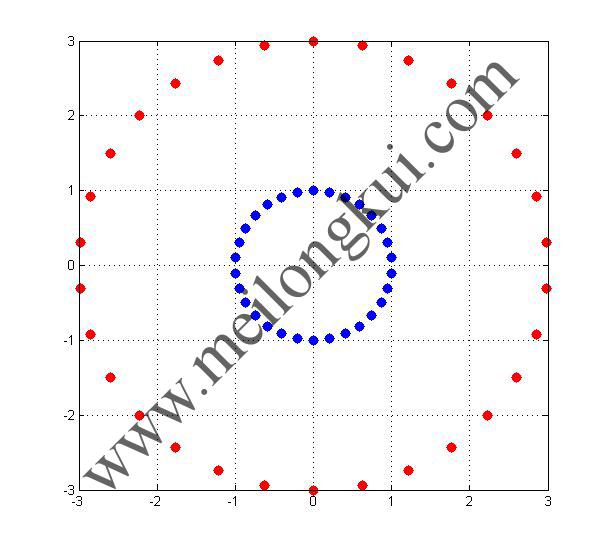
二维空间线性不可分示例
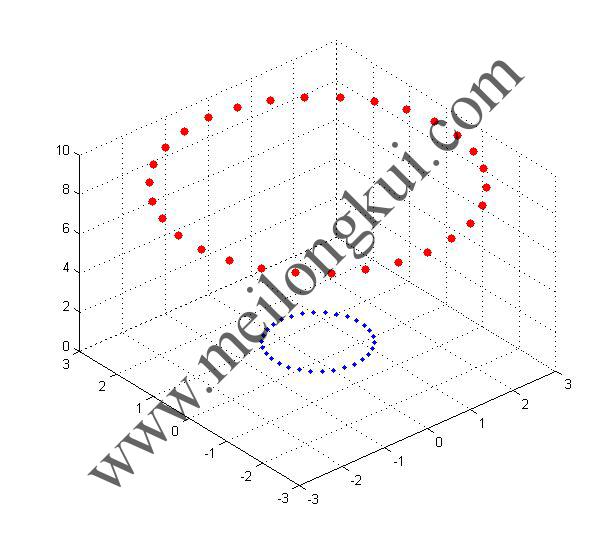
二维空间的线性不可分在三维空间变得可分
可以想象，如果我们非要不通过向高维映射的方式来解决线性不可分问题，那么可以通过引入多条直线（即引入多个线性分类器）的方式实现：
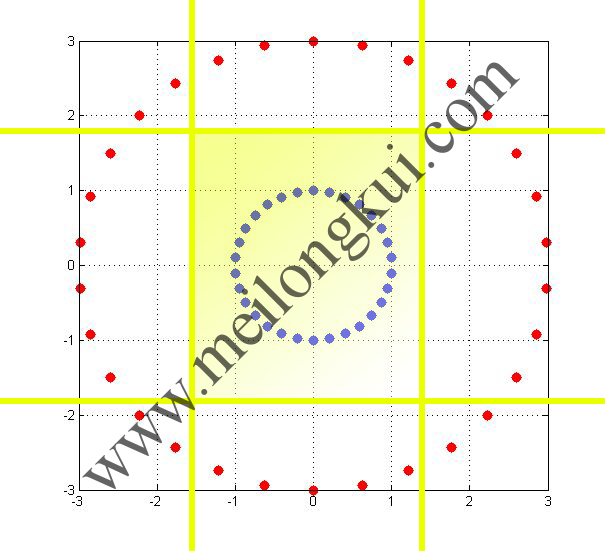
同时通过四条直线实现线性可分
在高维的复杂场景下，深度神经网络正是通过这种叠加海量线性分类器（和非线性分类器，后详）的思想实现的。
三、神经网络与深度神经网络
计算机领域中的神经网络特指人工神经网络（Artificial Neural Network，ANN），是一种人们受到生物神经细胞结构启发而研究出的一种算法体系。深度学习的实现是通过深度神经网络（Deep Neural Network，DNN）实现的。
1943年，Warren McCulloch和Walter Pitts提出了最早的神经网络数学模型，即The McCulloch-Pitts Model of Neuron。该结构大致模拟了人类神经元的工作原理，它们都有一些输入，然后将输入进行一些变换后得到输出结果。虽然人类目前对神经元处理输入信号的原理并没有完全的认知，但McCulloch-Pitts Neuron结构使用简单的线性加权和及阈值函数的方式来模拟这个变换，我们可以感性地发现生物神经元结构与McCulloch-Pitts Neuron结构的相似性：
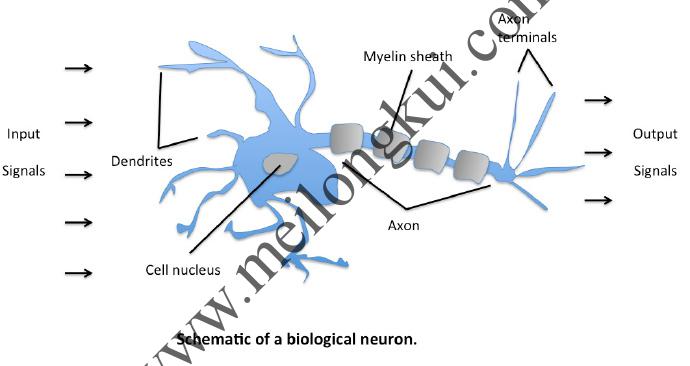
生物神经元
McCulloch-Pitts Neuron
我们在初中生物课上学习过，生物的神经网络是由无数个相互连接的神经元组成的，这些神经元通过树突（Dendrites）接收来自其他神经元的信号、通过细胞体（Soma）处理信息、通过轴突（Axon）传输这个神经元的输出、通过突触（Synapse）与其他神经元连接在一起，每个神经元只有在满足其各自的标准时才会被激活：
生物神经网络示意
很明显，如果要使用McCulloch-Pitts Neuron模型，那么我们就需要对结构中的各个权重进行设置。不过，通过人类经验设置权重是麻烦且很难达到最优的，因此1958年Frank Rosenblatt提出了第一个能够根据样本数据来学习特征权重的感知机模型（Perceptron）。不过，由于当时计算能力的限制，实现多层的神经网络是不可能的，因此导致了整个学术届对生物启发的机器学习模型的抨击，导致了神经网络的发展进入了一次重大低潮期。
2010年之后，随着计算机性能的进一步提高以及云计算、GPU的迅猛发展，使得计算量已经不再是阻碍神经网络发展的问题。同时，随着互联网+的发展，获取海量数据也不再困难，因此让神经网络所面临的几个最大问题都得到解决，神经网络的发展从而也迎来了新的高潮。
四、现代神经元
一个现代神经元通常由线性模型和激励/激活函数（activation function）两部分组成，其中激励函数紧跟在线性模型后，用来加入非线性因素。一个线性模型为最普通的一次函数组成的神经元为：
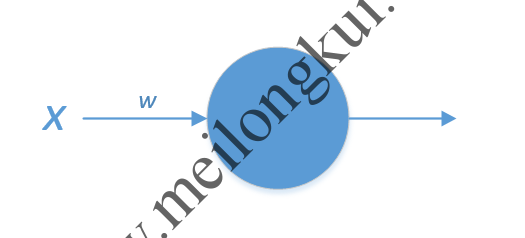
最简单的神经元
可表达为：
![\[f(x)=wx+b\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-f01cd72cb5f525e26aa4b4e40dedaf8b_l3.png "Rendered by QuickLaTeX.com")
当x为一个多维的n维向量时，则建立了一个有n个输入的项的神经元：
![\[f(x)=f(x_{1},x_{2},...,x_{2})\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-1f9f72dd4eb3095c8ad234206e30f5d4_l3.png "Rendered by QuickLaTeX.com")
将其记为
5个输入项的神经元
其中x是一个1×n的矩阵，w是一个n×1的权重矩阵，b是一个称为偏置（bias）的实数。wx是两个矩阵进行内积，结果是一个实数，再加上一个实数b，结果认为一个实数。
这个函数是神经元对x最为核心的线性处理部分，其中x即所谓的特征向量，表示了对一个样本的描述，这个描述是多个维度的描述，每个维度指代的含义在不同场景下对应不同的解释。接下来，让我们用一个可以简单的实例建立感性的认识。
五、金融机构客户信用评级的简单例子
下面，以金融机构客户信用评级这个场景，举一个简单示例来建立大致的感性认识。假设按如下的5个维度（性别、年龄、年收入、用户忠诚度指数、负债）：
![\[ \left[ {\begin{array}{cc} Gender \\ Age \\ Income \\ Loyalty \\ Debt \end{array} } \right] \]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-29de42faf064a8e6ff87923cc5a22b11_l3.png "Rendered by QuickLaTeX.com")
建立特征向量x：
![\[ \left[ {\begin{array}{cc} 1\\ 20\\ 27\\ 19\\ -55 \end{array} } \right] \]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-2374a696f356d6f816f0788c0befb3dd_l3.png "Rendered by QuickLaTeX.com")
来描述某个客户的个人信用情况。w是一个n×1的矩阵，表示各维度所占的权重，如[0.3 0.8 1.5 1.2 0.5]分别表示[性别权重 年龄权重 年收入权重 用户忠诚指数权重 负债权重]，那么f(x)=wx+b即为评价客户信用风险的评价函数。先假设b为零，上例的结果即为：
![\[f(x)=1\times 0.3+25\times 0.8+10\times 1.5+19 \times 1.2+(-55) \times 0.5+0\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-9ef366554182b6cc98a06a099c59a9bc_l3.png "Rendered by QuickLaTeX.com")
感性地看，实际上f(x)=wx+b通过权重值和偏置决定了每个维度特征对最终结果的影响程度。这样一来，用户信用评级的核心问题就变成了如何确定权重的问题。比如，我们可以通过多年的业务经验总结，由业务专家给出先验性的值——这显然是很可能很困难、不准确身在在某些问题上不可能的；也以通过机器学习方式来确定权重。
不管用哪种方法确定了权重值，在我们具有了大量样本的特征向量后，都可以描述拟合与真实观测之间的差异，这是通过损失函数Loss来进行的：
![\[Loss=\sum_{i=1}^n | wx_{i}+b-yi|\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-7ca079b425c3af1cfda07b086cbf1e8c_l3.png "Rendered by QuickLaTeX.com")
拟合与真实观测之间的差异之和（注意此处的绝对值）即称为残差。如果想要得到比较合适的w和b，那么实际就是需要让函数
![\[Loss(w,b)\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-f4064399561edc0de304ac31224882b3_l3.png "Rendered by QuickLaTeX.com")
尽可能小。
六、激活函数引入的非线性因素
生物科学证明，当生物神经网络中的神经元在处理某一项任务时，某些神经元会异常活跃，而某些神经元则几乎不参与工作。激活函数在神经网络中引入了非线性学习和处理的能力，即可以感性地认为激活函数赋予了神经元不同程度激活的状态。可以认为，深度神经网络能力的提升不是因为增加了多层神经元，而是在于神经元中引入的激活函数，这是因为：
如果仅有线性函数来进行拟合的话，那么拟合的结果一定仅仅包含各种各样的线性关系，而客观的、要求解的问题本身一定不可能仅仅是简单的线性关系，因此仅有线性函数的网络必定是严重欠拟合的，因为从一开始设计出来的网络就有先天缺陷，一开始就猜错了问题本身的样子，那么再怎么训练都不会有好的结果。
激活函数需要满足非线性、可导（梯度下降时使用）和单调三个特性，常见的主要包括：
· Sigmoid函数
· Tanh函数
· ReLU（Rectified Linear Unit）函数
以最基础的Sigmoid函数为例，其定义为：
![\[f(x)=\frac{1}{1+e^{-(wx+b)}}\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-2e80526cce72ad883647d24c3a199e25_l3.png "Rendered by QuickLaTeX.com")
或者也可以写成：
![\[z=wx+b,f(z)=\frac{1}{1+e^{-z}}\]](http://www.meilongkui.com/wp-content/ql-cache/quicklatex.com-29c601ec04083fa496c0fc727e1d598d_l3.png "Rendered by QuickLaTeX.com")
其对应的函数图像为：
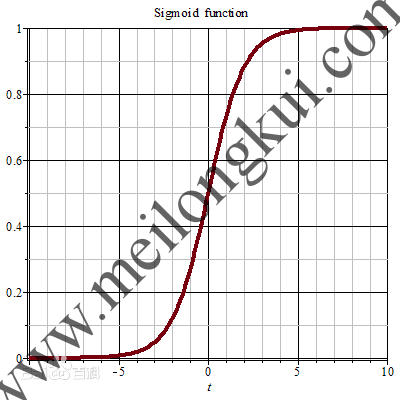
Sigmoid函数
其中横轴是z、纵轴是f(z)。Sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。在这个函数图像中，我们会发现，对于一个高维的输入特征向量x，在wx两个矩阵进行完内积再加上b后，线性模型的结果又充当自变量z叠加到了f(z)=中，使得结果不再是单纯的线性关系，而最终变成了0-1之间不同程度的激活（1为完全激活、0为完全不激活）：
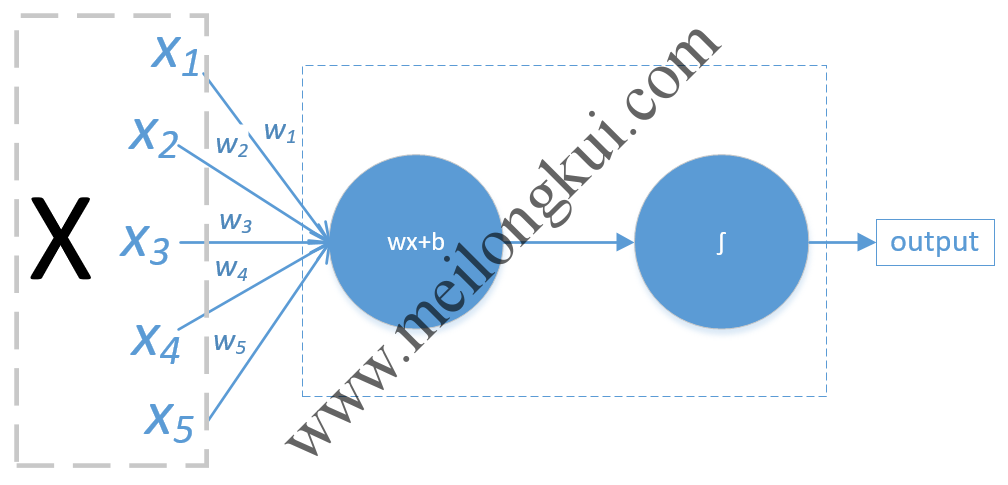
Sigmoid函数示意
上图中x只画了5条线，但现实中的全连接网络x可能有几万条线不止。
其他的激活函数也很重要，后续会逐渐用到，再总结，在此不展开。
七、深度神经网络与线性不可分问题的解决
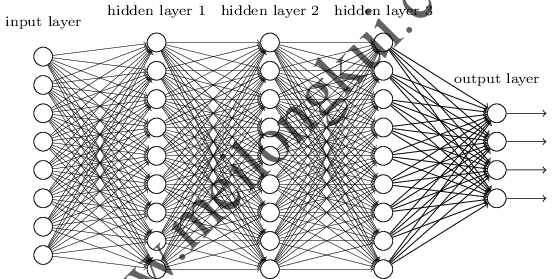
一个全连接的深度神经网络
当多个神经元首尾连接形成一个网络结构来协同工作的时候就可以被称为神经网络了。神经网络一般分为输入层（input layer）、隐藏层/隐含层（hidden layer）和输出层（output layer）。其中，输入层位于整个网络的最前端，直接接受输入的向量而不对数据做任何处理，因此一般不计入层数；输出层位于整个网络的最后一层，用来输出整个网络处理的值，这个值可能是一个分类向量值，也可能是一个类似线性回归那样产生的连续的值，也可能是别的复杂类型的值或者向量。根据不同的需求，输出层的构造也不尽相同。
由于神经网络的神经元可以有很多层，每层又可以有很多个神经元，所以整个网络的规模可以有几千甚至几万个神经元。在这种情况下，我们几乎可以描绘出任意的线性不可分的模型。在文本的第二部分中，我们只是用了一个简单的二维向量来进行说明；但是，真正的商用场景中，这些向量通常有几十万个纬度甚至更多，神经网络的层数也会非常深。随着维度的加大，深度的加深，网络所能描述的分类器的复杂程度也随之增强，所以传统分类模型中无法通过简单的线性分离器和非线性分类器处理的复杂学习场景（例如图形、音频、视频等），就能够通过海量分类器的叠加来实现了。
八、问题转化为了要确定哪些权重和如何确定权重
到这里，我们就可以感性地认识到，问题转换成了要确定哪些权重（即如何组织网络）和如何确定权重（即如何通过训练得到恰当的权重值），后详。
参考资料：
1、《白话深度学习与TensorFlow》，机械工业出版社；
2、《TensorFlow-实战Google深度学习框架》，电子工业出版社；
3、《深入浅出深度学习-原理剖析与Python实践》，电子工业出版社；
4、《机器学习实战》，人民邮电出版社；
5、《达特茅斯会议:人工智能的缘起》，https://www.sohu.com/a/63212045_117499
6、《一篇文章讲清楚人工智能、机器学习和深度学习的区别和联系》，http://blog.sciencenet.cn/blog-2888249-1082369.html
7、《如何理解在二维空间内线性不可分的数据，可以在五维空间内线性可分》，https://www.zhihu.com/question/27210162
8、《SVM清晰讲解——线性可分问题》、https://www.cnblogs.com/fuqia/p/8963429.html
9、《The McCulloch-Pitts Model of Neuron》，http://wwwold.ece.utep.edu/research/webfuzzy/docs/kk-thesis/kk-thesis-html/node12.html
10、《McCulloch-Pitts Neuron - Mankind’s First Mathematical Model Of A Biological Neuron》，https://towardsdatascience.com/mcculloch-pitts-model-5fdf65ac5dd1
11、https://baike.baidu.com/item/Sigmoid%E5%87%BD%E6%95%B0/7981407?fr=aladdin
转载时请保留出处，违法转载追究到底：进城务工人员小梅 » 深度学习基础知识半感性小结1-从线性不可分问题的解决到金融机构信用评级的感性示例