RSA中公钥和私钥到底哪个才是用来加密和哪个用来解密

问题一：为何SM2只能公钥加密，而同样是非对称加密的RSA却公钥私钥均可用于加密；
问题二：既然RSA可以“私钥加密公钥解密、公钥加密私钥解密”，但是实践中为何总是“公钥加密私钥解密”，即知乎问题：https://www.zhihu.com/question/25912483；

对于第一个问题首先是ECC与RSA的数学原理不同。公开密钥算法总是要基于一个数学上的难题，比如RSA依靠的是：给定两个素数/质数p、q很容易相乘得到n，而对n进行因式分解却相对困难。

第一步，随机选择两个不相等的互质质数p和q（即p和q的公约数只有1，实际应用中会选择很大的质数）。

例如，p=61，q=53。

第二步，计算p和q的乘积n。

　　n = p×q = 61×53 = 3233

3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。实际应用中，RSA密钥一般是1024位、2048位等。

第三步，计算p和q的欧拉n，φ(n)。

　　φ(n) = (p-1)×(q-1) = 60×52 = 3120

第四步，随机选择一个整数e，要求1< e < φ(n)且e与φ(n) 互质，即e与φ(n)的公约数只有1。

e可选择的有很多，例如17。
根据知乎问题中的某个回答，e常常取65537，其原因在于：
1）65537和φ(n)互质的概率更高；
2）为了加密速度，因为65537是0x10001；
在参考文档3中也有说明。

第五步，计算e对于φ(n)的模反元素d。

所谓”模反元素”，就是指有一个整数d，可以使得ed被φ(n)除的余数为1。

　　ed % φ(n) = 1

这个式子等价于

　　ed = kφ(n) + 1，其中k为系数且从1开始

这样：

　　d = (kφ(n) + 1) ÷ e = (k×3120 + 1) ÷ 17，必须能除尽且没有余数

当k=15时，d=2753。验证要求：

　　ed % φ(n) = 17 × 2753 % 3120 = 1

另外，求d也可以使用“扩展欧几里得算法”求解。即求模反元素d实质上就是对下面这个二元一次方程求解：

　　ex + φ(n)y = 1

已知 e=17，φ(n)=3120：

　　17x + 3120y = 1

算出一组整数解为(x,y)=(2753,-15)，即 d=2753。

第六步，n和e，n和d即为一对密钥。

在实际应用中，公钥和私钥的数据都采用ASN.1格式。上例中，n=3233，e=17，d=2753，所以公钥为(3233,17)，私钥为(3233,2753)。
假设密钥A为n和e，密钥B为n和d，n联系起了公钥和私钥。
用钥匙A加密123：

　　123 ** e % n = 123 ** 17 % 3233 = 855

用钥匙B解密855：

　　855 ** d % n = 855 ** 2753 % 3233 = 123

用钥匙B加密99：

　　99 ** d % n = 99 ** 2753 % 3233 = 89

用钥匙A解密89：

　　89 ** e % n = 89 ** 17 % 3233 = 99

可见，从数学上讲随机数e和d是对等的（而非pq是对等的）。在RSA的代码实现中，我们也会发现公私钥均可用于加密，也就是常说的：

私钥加密公钥可以解密

公钥加密私钥可以解密

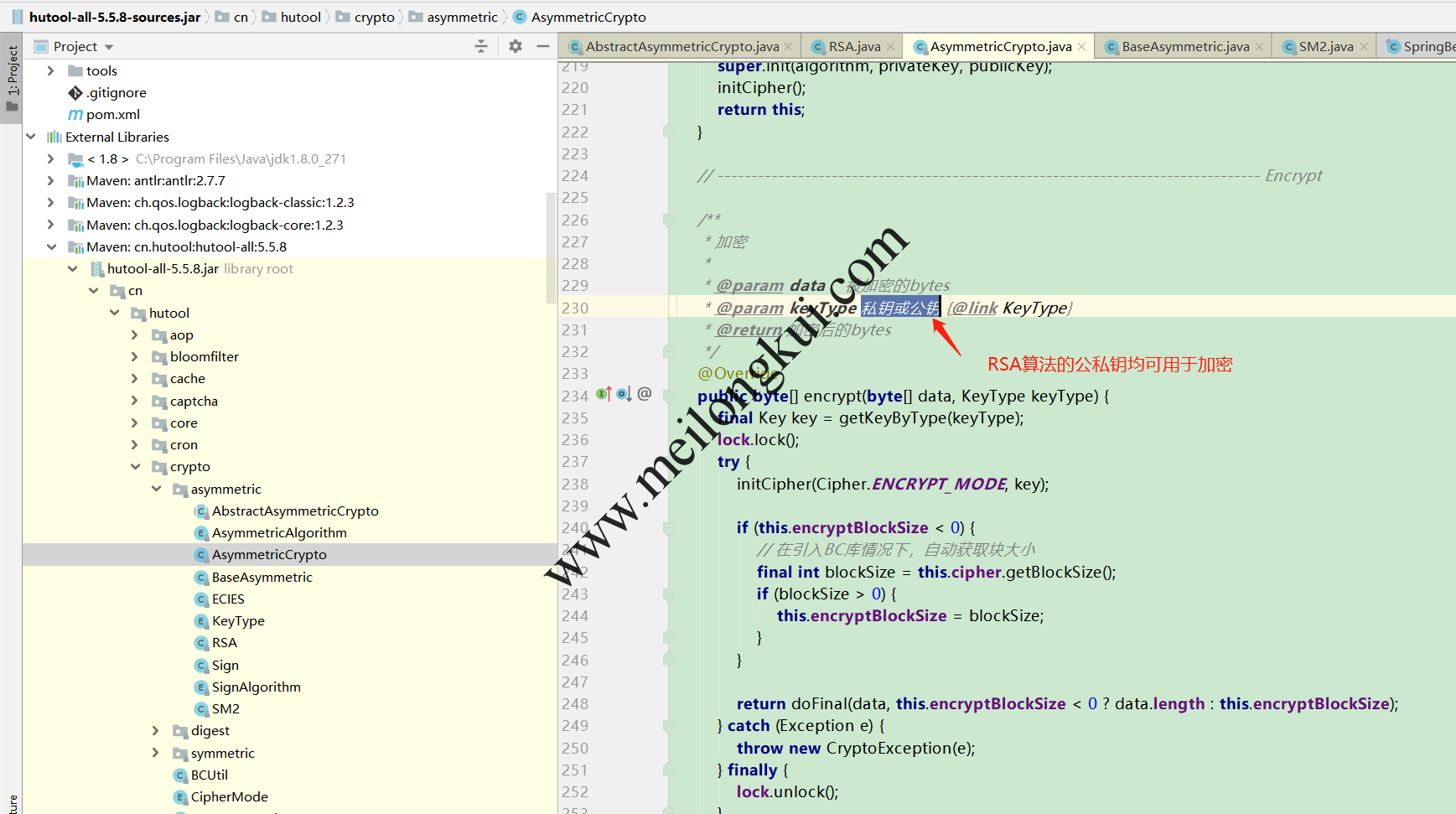
但是，要注意：
0）从直觉上看，如果用e=17当私钥，d=2753当公钥，那么私钥可以在很短的时间内被穷举出来。因此在实际使用中e和d的选择是有条件的，私钥一定是一个满足一定条件、在短时间内无法暴力破解的数；
1）在很多情况下，e取65537（0x10001），也就是第五个费马数，所以不能把e作为私钥。至于e为什么选择0x10001原因见参考文档3和参考文档4。
2）与ECC不同，RSA只有私钥求不出公钥。不过，由于一般公钥的e都是65537且OpenSSL等生成的私钥带着p,q,e,d,n等等的信息（本质上是一对密钥，如下所示），所以从私钥中提取指数e（65537）和模n就组成了公钥。我们可以很容易地造一个私钥，然后解析：

RFC 2347中RSA私钥的ASN.1定义：

此外，这里的855的2753次方结果非常大，已经超出了一般的变量可表示的最大值，计算机里一般大数用科学记数法给出的是近似值，那么这之后如何进行精确的计算呢？知乎的答案里面有：

RSA数字签名的“签名”过程本身也就是加密过程。签名时，对原文的摘要（哈希值）用私钥进行加密处理，以达到他人不可伪造的效果。而在验证签名时，先用相应的公钥解出信息宣称的摘要A，然后再用发信人公布的哈希函数根据原文解出摘要B，只要A和B一致就可确定原文未被篡改（完整性），且确实为发信人所发（不可抵赖，在不知道私钥的情况下不可能正确签名，错误的签名被解密后无法得到正确的摘要）。

七、RSA算法的可靠性

在密钥生成步骤中一共出现的六个数字：

p
q
n
φ(n)
e
d

中公钥用到了两个n和e，其余四个数字都不公开。其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。另外，d的大小要求应该是大于N^0.292，低于这个大小都能比较快的解出来。0.292来自1-sqrt(0.5)。

那么，有无可能在已知n和e的情况下，推导出d？

（1）ed % φ(n) = 1。只有知道φ(n)，才能算出d。

（2）φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。

（3）n=pq。只有将n因数分解，才能算出p和q。

结论：如果n可以被因数分解，d就可以算出，也就意味着私钥被破解。

可是，大整数的因数分解，是一件非常困难的事情。目前，除了暴力破解，还没有发现别的有效方法。维基百科这样写道：

对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。

假如有人找到一种快速因数分解的算法，那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。

只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。

举例来说，你可以对3233进行因数分解（61×53），但是你没法对下面这个整数进行因数分解。

12301866845301177551304949
58384962720772853569595334
79219732245215172640050726
36575187452021997864693899
56474942774063845925192557
32630345373154826850791702
61221429134616704292143116
02221240479274737794080665
351419597459856902143413

它等于这样两个质数的乘积：

33478071698956898786044169
84821269081770479498371376
85689124313889828837938780
02287614711652531743087737
814467999489
×
36746043666799590428244633
79962795263227915816434308
76426760322838157396665112
79233373417143396810270092
798736308917

事实上，这大概是人类已经分解的最大整数（232个十进制位，768个二进制位）。比它更大的因数分解，还没有被报道过，因此目前被破解的最长RSA密钥就是768位。

聚焦到前两个问题，实际上需要拆分成：
1、算法层面e和d的选择问题。随机数e和d虽然在数学层面等价，但实际中选择d作为私钥，而非e作为私钥；
2、实际层面的使用方式问题。站在信息机密性的角度看，公钥加密方案的初衷就是为了公开加密密钥，让所有人都可以给某个人发送消息，其密码学的假设是“一个合格的加密方案，敌手拿到密文c不能恢复出明文m”，因此私钥加密公钥解密时所有人都将能够解密信息，有悖于密码学假设。但是，如果结合数字签名的角度看，在签名算法中私钥用于对数据进行签名，公钥用于对签名进行验证（也可以直观地进行理解：对一个文件签名，当然要用私钥，因为我们希望只有自己才能完成签字。验证过程当然希望所有人都能够执行，大家看到签名都能通过验证证明确实是我自己签的），那么发行方发行了一对公私钥对并公开公钥后，如果私钥加密公钥解密那就保证了只有发行方可写从而验证发行方身份；如果公钥加密私钥解密，那就保证了只有发行方可读从而保证递交给发行方的信息不会被他人窃取。

参考文档：
1、https://www.zhihu.com/question/25912483
2、http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html，最后有数学证明（费尔马小定义）
3、https://en.wikipedia.org/wiki/65,537#:~:text=65537%20is%20commonly%20used%20as,4%22%20or%20%22F4%22.
4、https://baike.baidu.com/item/%E8%B4%B9%E9%A9%AC%E6%95%B0/8080264?fr=aladdin
5、https://blog.csdn.net/qq_38313548/article/details/85387466

转载时请保留出处，违法转载追究到底：进城务工人员小梅 » RSA中公钥和私钥到底哪个才是用来加密和哪个用来解密