MySQL层次关系的存储，预排序树（Modified Preorder Tree）的原理、实现与使用-进城务工人员小梅

我们常常用树形结构来表征数据的层次关联关系，如机构、账户树、商品品类、新闻栏目等。由于传统关系数据库使用的是二维表，因此在持久化时就涉及到这类层次关系的存储问题，需要设计合理的表结构及CRUD算法，并保证：
1、相对可理解；
2、冗余数据少；
3、查询简单高效；
4、节点增删改查CRUD操作高效；

一、邻接表模型（Adjacency list model）
邻接表模型是存储层次结构最简单和直观的做法，只需要在每个节点中多加一个指向上级节点的字段parent即可实现上下级节点的关联（最上层节点的parent为NULL），如：

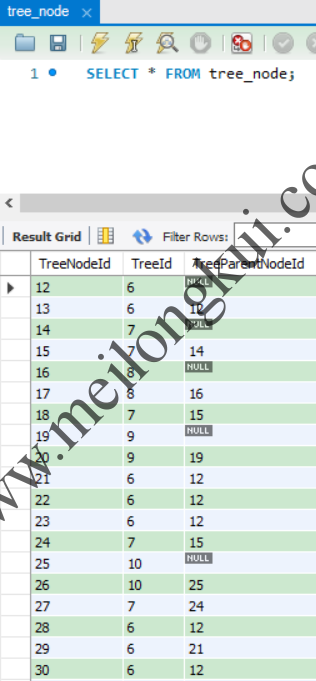
邻接表实现举例

邻接表模型的存储通常只需要一张二维关系表，当级层关系倾向于横向发展时此种实现相对高效，但当层级关系倾向于纵向发展的话则此种实现会较为痛苦。由于仅仅记录了节点之间的上下级关系，因此在当出现“查找某个节点的上下级/祖先/后代”之类的场景时就必须进行递归，而在递归过程所涉及的数据库I/O导致了CRUD操作的低效，且递归的过程不易使用纯SQL语句实现。即使某些优化过的邻接存储方案，在修改操作时也容易出现写逻辑放大的问题。
受限于此，邻接存储的实现通常用于层次模型规模相对较小、CRUD操作相对较少的情况下。在日常的应用中，我们常常会使用一些技巧对邻接表模型进行优化，例如：
1、进行一定程度的反范式化处理，通过在表中增加诸如根节点、节点所在层级等冗余字段来优化特定场景的查询需求；
2、在某些不要求严格一致性业务场景下，借助缓存机制等避免递归过程中直接对数据库进行操作导致的性能开销；

二、改进的预排序树（Modified preorder tree）
在一般的业务场景下，查询操作总是多于插入、修改和删除操作。预排序树是为了避免对于层次结构查询时的递归操作而基于前序遍历实现的一种查询无递归、支持无限分组的左右值编码方案。以《Managing Hierarchical Data in MySQL》中的电子商店的产品分类为例：

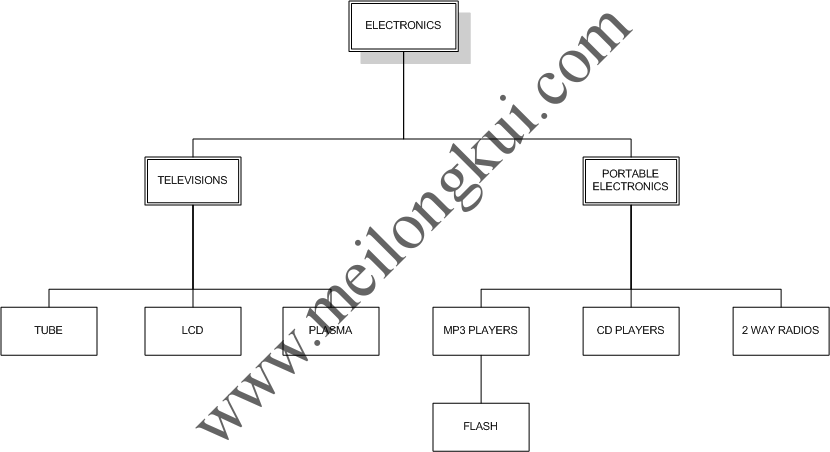
层次结构示例

通过嵌套集合模型（Nested set model）以嵌套容器的方式画出上述产品分类如下：

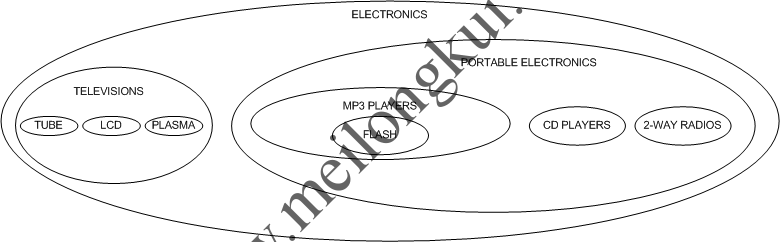
使用嵌套集合模型表示的层次结构示例

上图依旧保持了数据的层次，父分类包围了其子分类。在数据表中，我们通过使用表示节点的嵌套关系的左值（left value）和右值（right value）来表现嵌套集合模型中数据的分层特性：

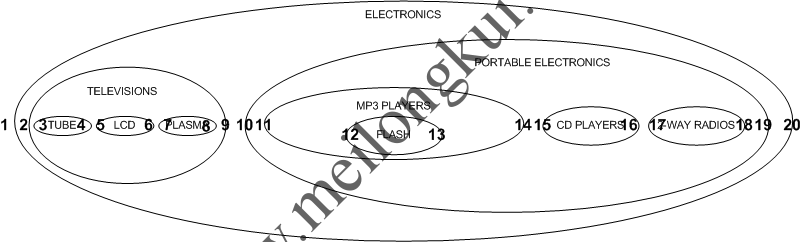
使用嵌套集合模型表示的层次结构示例2

由于left和right是MySQL的保留字，因此我们使用lft和rgt来分别代替left和right。从外层节点的最左侧开始，从左到右依次编号，就得到了一颗对应的树状结构：

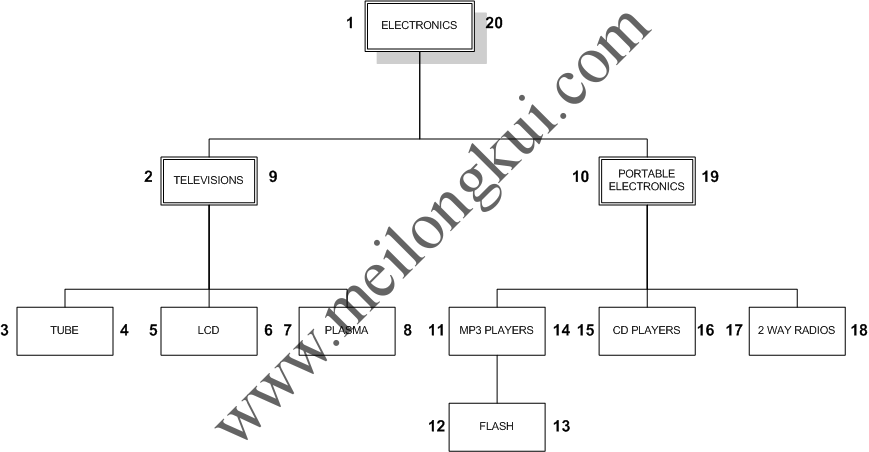
使用预排序树表示的层次结构示例

当按照从左到右、一次一层的先序遍历规则为节点赋左、右值时，由于一个节点上被赋了两个值，因此这种方法被称作改进的先序遍历算法（Modified preorder tree traversal algorithm）。预排序树的每一个节点都有一个“左值”和“右值”，且满足如下的规则：
1、后代节点的左值总是大于祖先节点的左值、后代节点的右值总是小于祖先节点的右值；
2、任意节点的右值总是大于左值；
3、叶节点的右值-左值=1；
4、非叶节点的右值-左值>1（对于仅由一个根节点构成的树，根节点是否是叶节点依赖于上下文）；

再如，如下的食品层次结构：

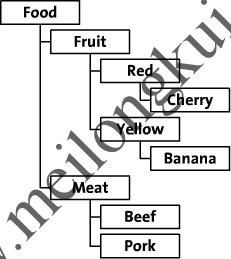
另一个层次结构示例

的预排序树表示为：

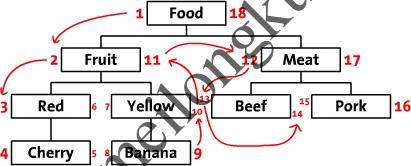
另一个层次结构示例的预排序树表示

其对应的数据库表为：

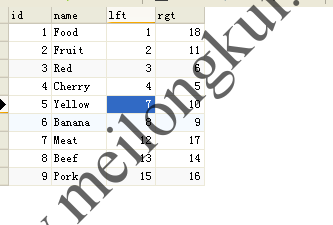
另一个层次结构示例的预排序树表示的数据库存储

再如：

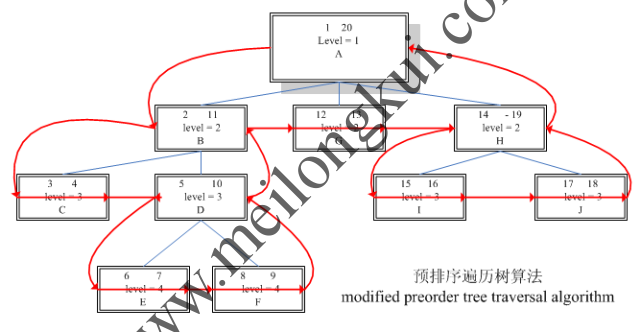
再一个层次结构示例的预排序树表示

对于层次结构所涉及的一些查询而言，改进的预排序树具有如下几点优良的特性：
1、与邻接表模型一样，支持无限分组；
2、不需要递归，即可快速查询任意节点的祖先或后代；
3、查询条件大多是基于整形的比较，效率较高；

三、预排序遍历树的重要操作
接下来，让我们依次梳理预排序遍历树的重要操作。我们以《Managing Hierarchical Data in MySQL》中的电子商店的产品分类为例进行说明，其基础SQL为：

CREATE TABLE nested_category (
    category_id INT AUTO_INCREMENT PRIMARY KEY,
    name VARCHAR(20) NOT NULL,
    lft INT NOT NULL,
    rgt INT NOT NULL
);

INSERT INTO nested_category VALUES(1,'ELECTRONICS',1,20);
INSERT INTO nested_category VALUES(2,'TELEVISIONS',2,9);
INSERT INTO nested_category VALUES(3,'TUBE',3,4);
INSERT INTO nested_category VALUES(4,'LCD',5,6);
INSERT INTO nested_category VALUES(5,'PLASMA',7,8);
INSERT INTO nested_category VALUES(6,'PORTABLE ELECTRONICS',10,19);
INSERT INTO nested_category VALUES(7,'MP3 PLAYERS',11,14);
INSERT INTO nested_category VALUES(8,'FLASH',12,13);
INSERT INTO nested_category VALUES(9,'CD PLAYERS',15,16);
INSERT INTO nested_category VALUES(10,'2 WAY RADIOS',17,18);

SELECT * FROM nested_category ORDER BY category_id;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           2 | TELEVISIONS          |   2 |   9 |
|           3 | TUBE                 |   3 |   4 |
|           4 | LCD                  |   5 |   6 |
|           5 | PLASMA               |   7 |   8 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+

CREATE TABLE nested_category (

category_id INT AUTO_INCREMENT PRIMARY KEY,

name VARCHAR(20) NOT NULL,

lft INT NOT NULL,

rgt INT NOT NULL

);

INSERT INTO nested_category VALUES(1,'ELECTRONICS',1,20);

INSERT INTO nested_category VALUES(2,'TELEVISIONS',2,9);

INSERT INTO nested_category VALUES(3,'TUBE',3,4);

INSERT INTO nested_category VALUES(4,'LCD',5,6);

INSERT INTO nested_category VALUES(5,'PLASMA',7,8);

INSERT INTO nested_category VALUES(6,'PORTABLE ELECTRONICS',10,19);

INSERT INTO nested_category VALUES(7,'MP3 PLAYERS',11,14);

INSERT INTO nested_category VALUES(8,'FLASH',12,13);

INSERT INTO nested_category VALUES(9,'CD PLAYERS',15,16);

INSERT INTO nested_category VALUES(10,'2 WAY RADIOS',17,18);

SELECT * FROM nested_category ORDER BY category_id;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 2 | TELEVISIONS | 2 | 9 |

| 3 | TUBE | 3 | 4 |

| 4 | LCD | 5 | 6 |

| 5 | PLASMA | 7 | 8 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

3.1 求整棵树所有节点的个数
由于每个节点各有一个左值和右值，且是从1开始计数的，因此根节点的右值除以2直接可以得到求整棵树所有节点的个数。以产品分类层次结构为例，根节点的右值为20，因此总节点数量=20÷2=10，对应的SQL形如：

SELECT (rgt div 2) AS total_node_count FROM nested_category
WHERE name='ELECTRONICS';
+------------+
| node_count |
+------------+
|         10 |
+------------+
1 row in set (0.02 sec)

SELECT (rgt div 2) AS total_node_count FROM nested_category

WHERE name='ELECTRONICS';

+------------+

| node_count |

+------------+

| 10 |

+------------+

1 row in set (0.02 sec)

3.2 求某个节点的后代个数（不含自身）
某个节点的后代个数（不含自身）=该节点的(右值-左值+1)÷2-1。例如，求PORTABLE ELECTRONICS后代个数的SQL形如：

SELECT ((rgt -lft + 1) div 2) -1 AS child_node_count FROM nested_category
WHERE name='PORTABLE ELECTRONICS';
+------------------+
| child_node_count |
+------------------+
|                4 |
+------------------+
1 row in set (0.05 sec)

SELECT ((rgt -lft + 1) div 2) -1 AS child_node_count FROM nested_category

WHERE name='PORTABLE ELECTRONICS';

+------------------+

| child_node_count |

+------------------+

| 4 |

+------------------+

1 row in set (0.05 sec)

3.3 求子树所有节点的个数
求子树所有节点的个数即求某个节点的后代个数（包含自身）=该节点的(右值-左值+1)÷2。例如，求PORTABLE ELECTRONICS后代个数的SQL形如：

SELECT ((rgt -lft + 1) div 2) AS child_node_count FROM nested_category
WHERE name='PORTABLE ELECTRONICS';
+------------------+
| child_node_count |
+------------------+
|                5 |
+------------------+
1 row in set (0.05 sec)

SELECT ((rgt -lft + 1) div 2) AS child_node_count FROM nested_category

WHERE name='PORTABLE ELECTRONICS';

+------------------+

| child_node_count |

+------------------+

| 5 |

+------------------+

1 row in set (0.05 sec)

显然，求整棵树所有节点的个数是一个特例。
3.4 求所有叶节点
由于叶子节点的左右值是连续的，因此只要查找满足rgt-lft=1的节点即可。对应的SQL形如：

SELECT * FROM nested_category
WHERE rgt -lft = 1;
+-------------+--------------+-----+-----+
| category_id | name         | lft | rgt |
+-------------+--------------+-----+-----+
|           3 | TUBE         |   3 |   4 |
|           4 | LCD          |   5 |   6 |
|           5 | PLASMA       |   7 |   8 |
|           8 | FLASH        |  12 |  13 |
|           9 | CD PLAYERS   |  15 |  16 |
|          10 | 2 WAY RADIOS |  17 |  18 |
+-------------+--------------+-----+-----+
6 rows in set (0.02 sec)

SELECT * FROM nested_category

WHERE rgt -lft = 1;

+-------------+--------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+--------------+-----+-----+

| 3 | TUBE | 3 | 4 |

| 4 | LCD | 5 | 6 |

| 5 | PLASMA | 7 | 8 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+--------------+-----+-----+

6 rows in set (0.02 sec)

3.5 求所有有孩子的节点（非叶节点）
同理，只要不查找满足rgt-lft=1的节点即可。对应的SQL形如：

SELECT * FROM nested_category
WHERE rgt -lft != 1;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           2 | TELEVISIONS          |   2 |   9 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
+-------------+----------------------+-----+-----+
4 rows in set (0.02 sec)

SELECT * FROM nested_category

WHERE rgt -lft != 1;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 2 | TELEVISIONS | 2 | 9 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

+-------------+----------------------+-----+-----+

4 rows in set (0.02 sec)

3.6 求某个节点的所有后代（不包含指定节点）
由于预排序树中后代节点的左值总是大于祖先节点的左值、后代节点的右值总是小于祖先节点的右值，因此某个节点A的后代一定是那些左值>A.lft且右值<A.rgh的节点，即能被A包住的节点。例如，求PORTABLE ELECTRONICS所有后代（不含PORTABLE ELECTRONICS自己）的SQL形如：

SELECT * FROM nested_category
WHERE lft>(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS');
+-------------+--------------+-----+-----+
| category_id | name         | lft | rgt |
+-------------+--------------+-----+-----+
|           7 | MP3 PLAYERS  |  11 |  14 |
|           8 | FLASH        |  12 |  13 |
|           9 | CD PLAYERS   |  15 |  16 |
|          10 | 2 WAY RADIOS |  17 |  18 |
+-------------+--------------+-----+-----+
4 rows in set (0.02 sec)

SELECT * FROM nested_category

WHERE lft>(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS');

+-------------+--------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+--------------+-----+-----+

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+--------------+-----+-----+

4 rows in set (0.02 sec)

3.7 求某个节点的所有后代（包含指定节点）
同理，求PORTABLE ELECTRONICS所有后代（包含PORTABLE ELECTRONICS自己）的SQL形如：

SELECT * FROM nested_category
WHERE lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS');
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+

SELECT * FROM nested_category

WHERE lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS');

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

也可以利用《Managing Hierarchical Data in MySQL》中的自连接（self-join），形如：

SELECT node.* FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS';
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+
5 rows in set (0.12 sec)

SELECT node.* FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS';

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

5 rows in set (0.12 sec)

3.8 获取树的所有节点
同理，获取根节点的所有后代（包括根节点）即可获取树的所有节点。SQL形如：

SELECT * FROM nested_category
WHERE lft>=(SELECT lft FROM nested_category WHERE name='ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='ELECTRONICS');
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           2 | TELEVISIONS          |   2 |   9 |
|           3 | TUBE                 |   3 |   4 |
|           4 | LCD                  |   5 |   6 |
|           5 | PLASMA               |   7 |   8 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+
10 rows in set (10.67 sec)

SELECT * FROM nested_category

WHERE lft>=(SELECT lft FROM nested_category WHERE name='ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='ELECTRONICS');

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 2 | TELEVISIONS | 2 | 9 |

| 3 | TUBE | 3 | 4 |

| 4 | LCD | 5 | 6 |

| 5 | PLASMA | 7 | 8 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

10 rows in set (10.67 sec)

也可以利用《Managing Hierarchical Data in MySQL》中的自连接（self-join），形如：

SELECT node.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name = 'ELECTRONICS';
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           2 | TELEVISIONS          |   2 |   9 |
|           3 | TUBE                 |   3 |   4 |
|           4 | LCD                  |   5 |   6 |
|           5 | PLASMA               |   7 |   8 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+
10 rows in set (0.08 sec)

SELECT node.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name = 'ELECTRONICS';

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 2 | TELEVISIONS | 2 | 9 |

| 3 | TUBE | 3 | 4 |

| 4 | LCD | 5 | 6 |

| 5 | PLASMA | 7 | 8 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

10 rows in set (0.08 sec)

3.9 遍历树
若需遍历树，只需要按照lft对节点进行排序即可得到先序遍历的结果。SQL形如：

SELECT * FROM nested_category
WHERE lft>=(SELECT lft FROM nested_category WHERE name='ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='ELECTRONICS')
ORDER BY lft;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           2 | TELEVISIONS          |   2 |   9 |
|           3 | TUBE                 |   3 |   4 |
|           4 | LCD                  |   5 |   6 |
|           5 | PLASMA               |   7 |   8 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+
10 rows in set (10.67 sec)

SELECT * FROM nested_category

WHERE lft>=(SELECT lft FROM nested_category WHERE name='ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='ELECTRONICS')

ORDER BY lft;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 2 | TELEVISIONS | 2 | 9 |

| 3 | TUBE | 3 | 4 |

| 4 | LCD | 5 | 6 |

| 5 | PLASMA | 7 | 8 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

10 rows in set (10.67 sec)

也可以利用《Managing Hierarchical Data in MySQL》中的自连接（self-join），形如：

SELECT node.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name = 'ELECTRONICS'
ORDER BY lft;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           2 | TELEVISIONS          |   2 |   9 |
|           3 | TUBE                 |   3 |   4 |
|           4 | LCD                  |   5 |   6 |
|           5 | PLASMA               |   7 |   8 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+
10 rows in set (0.08 sec)

SELECT node.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name = 'ELECTRONICS'

ORDER BY lft;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 2 | TELEVISIONS | 2 | 9 |

| 3 | TUBE | 3 | 4 |

| 4 | LCD | 5 | 6 |

| 5 | PLASMA | 7 | 8 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

10 rows in set (0.08 sec)

3.10 获取子树的所有节点
获取子树的所有节点就是求某个节点的所有后代（包含指定节点）。例如，求PORTABLE ELECTRONICS子树所有节点的SQL形如：

SELECT * FROM nested_category
WHERE lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS');
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+

SELECT * FROM nested_category

WHERE lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS');

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

3.11 遍历子树
若需遍历子树，只需要按照lft对节点进行排序即可得到先序遍历的结果。SQL形如：

SELECT * FROM nested_category
WHERE lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS')
ORDER BY lft;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
|           9 | CD PLAYERS           |  15 |  16 |
|          10 | 2 WAY RADIOS         |  17 |  18 |
+-------------+----------------------+-----+-----+

SELECT * FROM nested_category

WHERE lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') and rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS')

ORDER BY lft;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

| 9 | CD PLAYERS | 15 | 16 |

| 10 | 2 WAY RADIOS | 17 | 18 |

+-------------+----------------------+-----+-----+

3.12 求某个节点的所有祖先（不包含指定节点）
同理，某个节点A的祖先一定是那些左值<A.lft且右值>A.rgh的节点，即能把A包住的节点。例如，求FLASH所有祖先（不含FLASH自己）的SQL形如：

SELECT * FROM nested_category
WHERE lft<(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>(SELECT rgt FROM nested_category WHERE name='FLASH');
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
+-------------+----------------------+-----+-----+
3 rows in set (0.02 sec)

SELECT * FROM nested_category

WHERE lft<(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>(SELECT rgt FROM nested_category WHERE name='FLASH');

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

+-------------+----------------------+-----+-----+

3 rows in set (0.02 sec)

3.13 求某个节点的所有祖先（包含指定节点）
例如，求FLASH所有祖先（包含FLASH自己）的SQL形如：

SELECT * FROM nested_category
WHERE lft<=(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH');
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
+-------------+----------------------+-----+-----+
4 rows in set (0.02 sec)y

SELECT * FROM nested_category

WHERE lft<=(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH');

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

+-------------+----------------------+-----+-----+

4 rows in set (0.02 sec)y

3.14 求某个节点到根节点的路径
由于能够获取到某个节点的所有祖先，因此只需要对这些祖先，根据lft进行降序排序即可得到从某个节点到根节点的路径。例如，求FLASH到根节点的SQL形如：

SELECT * FROM nested_category
WHERE lft<=(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH')
ORDER BY lft DESC;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           8 | FLASH                |  12 |  13 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           1 | ELECTRONICS          |   1 |  20 |
+-------------+----------------------+-----+-----+

SELECT * FROM nested_category

WHERE lft<=(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH')

ORDER BY lft DESC;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 8 | FLASH | 12 | 13 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 1 | ELECTRONICS | 1 | 20 |

+-------------+----------------------+-----+-----+

也可以利用《Managing Hierarchical Data in MySQL》中的自连接（self-join），形如：

SELECT parent.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'FLASH'
ORDER BY parent.lft DESC;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           8 | FLASH                |  12 |  13 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           1 | ELECTRONICS          |   1 |  20 |
+-------------+----------------------+-----+-----+
4 rows in set (0.09 sec)

SELECT parent.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'FLASH'

ORDER BY parent.lft DESC;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 8 | FLASH | 12 | 13 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 1 | ELECTRONICS | 1 | 20 |

+-------------+----------------------+-----+-----+

4 rows in set (0.09 sec)

3.15 求根节点到某个节点的路径
由于能够获取到某个节点的所有祖先，因此只需要对这些祖先，根据lft进行升序排序即可得到从根节点到某个节点的路径。例如，求根节点到FLASH的SQL形如：

SELECT * FROM nested_category
WHERE lft<=(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH')
ORDER BY lft;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
+-------------+----------------------+-----+-----+
4 rows in set (0.82 sec)

SELECT * FROM nested_category

WHERE lft<=(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH')

ORDER BY lft;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

+-------------+----------------------+-----+-----+

4 rows in set (0.82 sec)

也可以利用《Managing Hierarchical Data in MySQL》中的自连接（self-join），形如：

SELECT parent.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'FLASH'
ORDER BY parent.lft;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           1 | ELECTRONICS          |   1 |  20 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           8 | FLASH                |  12 |  13 |
+-------------+----------------------+-----+-----+
4 rows in set (0.08 sec)

SELECT parent.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'FLASH'

ORDER BY parent.lft;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 1 | ELECTRONICS | 1 | 20 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 8 | FLASH | 12 | 13 |

+-------------+----------------------+-----+-----+

4 rows in set (0.08 sec)

3.16 求某个节点的深度
在得到了某个节点到根节点的路径后，自然也就可以很容易地得到某个节点的深度（根节点深度为0）。例如，求FLASH的深度的SQL形如：

SELECT COUNT(1) AS node_depth FROM nested_category
WHERE lft<(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>(SELECT rgt FROM nested_category WHERE name='FLASH')
+------------+
| node_depth |
+------------+
|          3 |
+------------+
1 row in set (0.08 sec)

SELECT COUNT(1) AS node_depth FROM nested_category

WHERE lft<(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>(SELECT rgt FROM nested_category WHERE name='FLASH')

+------------+

| node_depth |

+------------+

| 3 |

+------------+

1 row in set (0.08 sec)

3.17 获取各个节点的深度
由于需要获取每个节点的深度和每个节点祖先的个数，因此必须使用自连接和GROUP。SQL形如：

SELECT node.name,COUNT(1) AS node_depth
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.category_id
ORDER BY node.lft;
+----------------------+------------+
| name                 | node_depth |
+----------------------+------------+
| ELECTRONICS          |          1 |
| TELEVISIONS          |          2 |
| TUBE                 |          3 |
| LCD                  |          3 |
| PLASMA               |          3 |
| PORTABLE ELECTRONICS |          2 |
| MP3 PLAYERS          |          3 |
| FLASH                |          4 |
| CD PLAYERS           |          3 |
| 2 WAY RADIOS         |          3 |
+----------------------+------------+
10 rows in set (0.19 sec)

SELECT node.name,COUNT(1) AS node_depth

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt

GROUP BY node.category_id

ORDER BY node.lft;

+----------------------+------------+

| name | node_depth |

+----------------------+------------+

| ELECTRONICS | 1 |

| TELEVISIONS | 2 |

| TUBE | 3 |

| LCD | 3 |

| PLASMA | 3 |

| PORTABLE ELECTRONICS | 2 |

| MP3 PLAYERS | 3 |

| FLASH | 4 |

| CD PLAYERS | 3 |

| 2 WAY RADIOS | 3 |

+----------------------+------------+

10 rows in set (0.19 sec)

3.18 获取树深度
各个节点中最大的深度既是树的深度。SQL形如：

SELECT MAX(T.node_depth)+1 AS tree_depth
FROM(SELECT node.name,COUNT(1) AS node_depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.category_id) AS T;
+------------+
| tree_depth |
+------------+
|          5 |
+------------+
1 row in set (0.10 sec)

SELECT MAX(T.node_depth)+1 AS tree_depth

FROM(SELECT node.name,COUNT(1) AS node_depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.category_id) AS T;

+------------+

| tree_depth |

+------------+

| 5 |

+------------+

1 row in set (0.10 sec)

3.19 带缩进地遍历整棵树
在有了所有节点的深度后，我们就可以利用深度信息，使用CONCAT和REPEAT函数来缩进地遍历整棵树。SQL形如：

SELECT CONCAT(REPEAT('-', COUNT(1) - 1), node.name) AS node_name
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.category_id
ORDER BY node.lft;
+-----------------------+
| node_name             |
+-----------------------+
| ELECTRONICS           |
| -TELEVISIONS          |
| --TUBE                |
| --LCD                 |
| --PLASMA              |
| -PORTABLE ELECTRONICS |
| --MP3 PLAYERS         |
| ---FLASH              |
| --CD PLAYERS          |
| --2 WAY RADIOS        |
+-----------------------+
10 rows in set (0.06 sec)

SELECT CONCAT(REPEAT('-', COUNT(1) - 1), node.name) AS node_name

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt

GROUP BY node.category_id

ORDER BY node.lft;

+-----------------------+

| node_name |

+-----------------------+

| ELECTRONICS |

| -TELEVISIONS |

| --TUBE |

| --LCD |

| --PLASMA |

| -PORTABLE ELECTRONICS |

| --MP3 PLAYERS |

| ---FLASH |

| --CD PLAYERS |

| --2 WAY RADIOS |

+-----------------------+

10 rows in set (0.06 sec)

3.20 求某个节点的父节点
在得到了某个节点到根节点的路径后，自然也就可以很容易地得到某个节点的父节点，只需要取出从该节点到根节点路径上的第一个节点即可。例如，求FLASH的父节点的SQL形如：

SELECT * FROM nested_category
WHERE lft<(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>(SELECT rgt FROM nested_category WHERE name='FLASH')
ORDER BY lft DESC
LIMIT 1;
+-------------+-------------+-----+-----+
| category_id | name        | lft | rgt |
+-------------+-------------+-----+-----+
|           7 | MP3 PLAYERS |  11 |  14 |
+-------------+-------------+-----+-----+
1 row in set (0.07 sec)

SELECT * FROM nested_category

WHERE lft<(SELECT lft FROM nested_category WHERE name='FLASH') and rgt>(SELECT rgt FROM nested_category WHERE name='FLASH')

ORDER BY lft DESC

LIMIT 1;

+-------------+-------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+-------------+-----+-----+

| 7 | MP3 PLAYERS | 11 | 14 |

+-------------+-------------+-----+-----+

1 row in set (0.07 sec)

3.21 获取子树各个节点的深度
先选出子树节点，然后对子树进行自连接和GROUP即可。例如，获取PORTABLE ELECTRONICS子树各节点深度的SQL形如：

SELECT sub_node.name,COUNT(1) AS sub_node_depth
FROM 
(SELECT node.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'
ORDER BY node.lft) AS sub_node, 
(SELECT node.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'
ORDER BY node.lft) AS sub_parent
WHERE sub_node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
GROUP BY sub_node.category_id
ORDER BY sub_node.lft;
+----------------------+----------------+
| name                 | sub_node_depth |
+----------------------+----------------+
| PORTABLE ELECTRONICS |              1 |
| MP3 PLAYERS          |              2 |
| FLASH                |              3 |
| CD PLAYERS           |              2 |
| 2 WAY RADIOS         |              2 |
+----------------------+----------------+
5 rows in set (0.11 sec)

SELECT sub_node.name,COUNT(1) AS sub_node_depth

FROM

(SELECT node.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'

ORDER BY node.lft) AS sub_node,

(SELECT node.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'

ORDER BY node.lft) AS sub_parent

WHERE sub_node.lft BETWEEN sub_parent.lft AND sub_parent.rgt

GROUP BY sub_node.category_id

ORDER BY sub_node.lft;

+----------------------+----------------+

| name | sub_node_depth |

+----------------------+----------------+

| PORTABLE ELECTRONICS | 1 |

| MP3 PLAYERS | 2 |

| FLASH | 3 |

| CD PLAYERS | 2 |

| 2 WAY RADIOS | 2 |

+----------------------+----------------+

5 rows in set (0.11 sec)

3.22 求某个节点的直接后代
有了子树各个节点的深度后，只需要使用HAVING筛出子树节点深度为1的节点既是对应节点的直接后代。例如，获取PORTABLE ELECTRONICS直接后代的SQL形如：

SELECT sub_node.name,COUNT(1)-1 AS sub_node_depth
FROM
(SELECT node.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'
ORDER BY node.lft) AS sub_node,
(SELECT node.*
FROM nested_category AS node, nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'
ORDER BY node.lft) AS sub_parent
WHERE sub_node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
GROUP BY sub_node.category_id
HAVING sub_node_depth=1
ORDER BY sub_node.lft;
+--------------+----------------+
| name         | sub_node_depth |
+--------------+----------------+
| MP3 PLAYERS  |              1 |
| CD PLAYERS   |              1 |
| 2 WAY RADIOS |              1 |
+--------------+----------------+
3 rows in set (0.06 sec)

SELECT sub_node.name,COUNT(1)-1 AS sub_node_depth

FROM

(SELECT node.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'

ORDER BY node.lft) AS sub_node,

(SELECT node.*

FROM nested_category AS node, nested_category AS parent

WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name='PORTABLE ELECTRONICS'

ORDER BY node.lft) AS sub_parent

WHERE sub_node.lft BETWEEN sub_parent.lft AND sub_parent.rgt

GROUP BY sub_node.category_id

HAVING sub_node_depth=1

ORDER BY sub_node.lft;

+--------------+----------------+

| name | sub_node_depth |

+--------------+----------------+

| MP3 PLAYERS | 1 |

| CD PLAYERS | 1 |

| 2 WAY RADIOS | 1 |

+--------------+----------------+

3 rows in set (0.06 sec)

3.23 求节点A到节点B的路径
只需要通过lft和rgh限制上下界即可。例如，求FLASH到PORTABLE ELECTRONICS路径的SQL形如：

SELECT * FROM nested_category
WHERE (lft<=(SELECT lft FROM nested_category WHERE name='FLASH') AND rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH'))
AND (lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') AND rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS'))
ORDER BY lft DESC;
+-------------+----------------------+-----+-----+
| category_id | name                 | lft | rgt |
+-------------+----------------------+-----+-----+
|           8 | FLASH                |  12 |  13 |
|           7 | MP3 PLAYERS          |  11 |  14 |
|           6 | PORTABLE ELECTRONICS |  10 |  19 |
+-------------+----------------------+-----+-----+
3 rows in set (0.50 sec)

SELECT * FROM nested_category

WHERE (lft<=(SELECT lft FROM nested_category WHERE name='FLASH') AND rgt>=(SELECT rgt FROM nested_category WHERE name='FLASH'))

AND (lft>=(SELECT lft FROM nested_category WHERE name='PORTABLE ELECTRONICS') AND rgt<=(SELECT rgt FROM nested_category WHERE name='PORTABLE ELECTRONICS'))

ORDER BY lft DESC;

+-------------+----------------------+-----+-----+

| category_id | name | lft | rgt |

+-------------+----------------------+-----+-----+

| 8 | FLASH | 12 | 13 |

| 7 | MP3 PLAYERS | 11 | 14 |

| 6 | PORTABLE ELECTRONICS | 10 | 19 |

+-------------+----------------------+-----+-----+

3 rows in set (0.50 sec)

3.24 插入节点
在层次结构中插入节点有几种方式，例如可以在兄弟节点之间插入等，但我们仅考虑在父节点下直接顺序追加兄弟节点的情况（即不考虑兄弟的顺序）。
由于插入节点涉及多步数据库操作，因此需要合理地使用锁和事务。以存储过程表示大致如下：

mysql> delimiter $$
mysql>
mysql> CREATE  PROCEDURE `append_child_to_parent_node`(IN `parent_category_node_id` INT,IN `new_node_name` VARCHAR(64))
    -> BEGIN
    ->    DECLARE rgt_id INT;
    ->    DECLARE t_error INT DEFAULT 0;
    ->    DECLARE CONTINUE HANDLER FOR SQLEXCEPTION SET t_error=1;
    ->    SELECT rgt INTO rgt_id FROM nested_category WHERE category_id= parent_category_node_id;
    ->    START TRANSACTION;
    ->         UPDATE nested_category SET rgt = rgt + 2 WHERE rgt >= rgt_id;
    ->         UPDATE nested_category SET lft = lft + 2 WHERE lft >= rgt_id;
    ->         INSERT INTO nested_category(name,lft,rgt) VALUES(new_node_name,rgt_id,rgt_id+1);
    ->     IF t_error =1 THEN
    ->      ROLLBACK;
    ->     ELSE
    ->       COMMIT;
    ->     END IF;
    -> END$$
Query OK, 0 rows affected (0.09 sec)

mysql>
mysql> delimiter ;
mysql>

mysql> delimiter $$

mysql>

mysql> CREATE PROCEDURE `append_child_to_parent_node`(IN `parent_category_node_id` INT,IN `new_node_name` VARCHAR(64))

-> BEGIN

-> DECLARE rgt_id INT;

-> DECLARE t_error INT DEFAULT 0;

-> DECLARE CONTINUE HANDLER FOR SQLEXCEPTION SET t_error=1;

-> SELECT rgt INTO rgt_id FROM nested_category WHERE category_id= parent_category_node_id;

-> START TRANSACTION;

-> UPDATE nested_category SET rgt = rgt + 2 WHERE rgt >= rgt_id;

-> UPDATE nested_category SET lft = lft + 2 WHERE lft >= rgt_id;

-> INSERT INTO nested_category(name,lft,rgt) VALUES(new_node_name,rgt_id,rgt_id+1);

-> IF t_error =1 THEN

-> ROLLBACK;

-> ELSE

-> COMMIT;

-> END IF;

-> END$$

Query OK, 0 rows affected (0.09 sec)

mysql>

mysql> delimiter ;

mysql>

我们在叶节点FLASH下增加一个名为FLASH FUCKING H5的节点，并观察插入该节点后的结构：

mysql> call append_child_to_parent_node((SELECT category_id FROM nested_category WHERE name='FLASH'),'FLASH FUCKING H5');
Query OK, 0 rows affected (0.09 sec)

mysql> SELECT CONCAT(REPEAT('*', COUNT(1) - 1), node.name) AS node_name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.category_id ORDER BY node.lft;
+-----------------------+
| node_name             |
+-----------------------+
| ELECTRONICS           |
| *TELEVISIONS          |
| **TUBE                |
| **LCD                 |
| **PLASMA              |
| *PORTABLE ELECTRONICS |
| **MP3 PLAYERS         |
| ***FLASH              |
| ****FLASH FUCKING H5  |
| **CD PLAYERS          |
| **2 WAY RADIOS        |
+-----------------------+
11 rows in set (0.09 sec)

mysql> call append_child_to_parent_node((SELECT category_id FROM nested_category WHERE name='FLASH'),'FLASH FUCKING H5');

Query OK, 0 rows affected (0.09 sec)

mysql> SELECT CONCAT(REPEAT('*', COUNT(1) - 1), node.name) AS node_name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.category_id ORDER BY node.lft;

+-----------------------+

| node_name |

+-----------------------+

| ELECTRONICS |

| *TELEVISIONS |

| **TUBE |

| **LCD |

| **PLASMA |

| *PORTABLE ELECTRONICS |

| **MP3 PLAYERS |

| ***FLASH |

| ****FLASH FUCKING H5 |

| **CD PLAYERS |

| **2 WAY RADIOS |

+-----------------------+

11 rows in set (0.09 sec)

然后在根节点ELECTRONICS下增加一个名为BIG SCREEN的节点，并观察插入该节点后的结构：

mysql> call append_child_to_parent_node((SELECT category_id FROM nested_category WHERE name='ELECTRONICS'),'BIG SCREEN');
Query OK, 0 rows affected (0.02 sec)

mysql> SELECT CONCAT(REPEAT('*', COUNT(1) - 1), node.name) AS node_name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.category_id ORDER BY node.lft;
+-----------------------+
| node_name             |
+-----------------------+
| ELECTRONICS           |
| *TELEVISIONS          |
| **TUBE                |
| **LCD                 |
| **PLASMA              |
| *PORTABLE ELECTRONICS |
| **MP3 PLAYERS         |
| ***FLASH              |
| ****FLASH FUCKING H5  |
| **CD PLAYERS          |
| **2 WAY RADIOS        |
| *BIG SCREEN           |
+-----------------------+
12 rows in set (0.02 sec)

mysql> call append_child_to_parent_node((SELECT category_id FROM nested_category WHERE name='ELECTRONICS'),'BIG SCREEN');

Query OK, 0 rows affected (0.02 sec)

+-----------------------+

| node_name |

+-----------------------+

| ELECTRONICS |

| *TELEVISIONS |

| **TUBE |

| **LCD |

| **PLASMA |

| *PORTABLE ELECTRONICS |

| **MP3 PLAYERS |

| ***FLASH |

| ****FLASH FUCKING H5 |

| **CD PLAYERS |

| **2 WAY RADIOS |

| *BIG SCREEN |

+-----------------------+

12 rows in set (0.02 sec)

3.25 删除节点
我们不考虑删除节点时对其后代节点进行继承等的情况，只考虑当删除节点时同时删除所有后代节点的情况。
在删除一个节点时，被删除节点的个数=(被删除节点的右值-被删除节点的左值+1)÷2，同时根据删除节点的数量修改剩余节点的左、右值。由于删除节点同样涉及多步数据库操作，因此也需要合理地使用锁和事务。以存储过程表示大致如下：

mysql> delimiter $$
mysql>
mysql> CREATE PROCEDURE `delete_node`(IN `category_id` INT)
    -> BEGIN
    ->    DECLARE lft_id INT;
    ->    DECLARE rgt_id INT;
    ->    DECLARE t_error INT DEFAULT 0;
    ->    DECLARE CONTINUE HANDLER FOR SQLEXCEPTION SET t_error=1;
    ->    SELECT lft,rgt INTO lft_id,rgt_id FROM nested_category WHERE nested_category.category_id=category_id;
    ->    START TRANSACTION;
    ->        DELETE FROM nested_category WHERE lft >= lft_id AND rgt <= rgt_id;
    ->        UPDATE nested_category SET lft = lft -(rgt_id - lft_id  + 1) WHERE lft > lft_id;
    ->        UPDATE nested_category SET rgt = rgt -(rgt_id - lft_id  + 1) WHERE rgt >rgt_id;
    ->     IF t_error =1 THEN
    ->      ROLLBACK;
    ->     ELSE
    ->       COMMIT;
    ->     END IF;
    -> END$$
Query OK, 0 rows affected (0.02 sec)

mysql>
mysql> delimiter ;
mysql>

mysql> delimiter $$

mysql>

mysql> CREATE PROCEDURE `delete_node`(IN `category_id` INT)

-> BEGIN

-> DECLARE lft_id INT;

-> DECLARE rgt_id INT;

-> DECLARE t_error INT DEFAULT 0;

-> DECLARE CONTINUE HANDLER FOR SQLEXCEPTION SET t_error=1;

-> SELECT lft,rgt INTO lft_id,rgt_id FROM nested_category WHERE nested_category.category_id=category_id;

-> START TRANSACTION;

-> DELETE FROM nested_category WHERE lft >= lft_id AND rgt <= rgt_id;

-> UPDATE nested_category SET lft = lft -(rgt_id - lft_id + 1) WHERE lft > lft_id;

-> UPDATE nested_category SET rgt = rgt -(rgt_id - lft_id + 1) WHERE rgt >rgt_id;

-> IF t_error =1 THEN

-> ROLLBACK;

-> ELSE

-> COMMIT;

-> END IF;

-> END$$

Query OK, 0 rows affected (0.02 sec)

mysql>

mysql> delimiter ;

mysql>

我们删除名为FLASH的节点，并观察删除该节点后的结构：

mysql> call delete_node((SELECT category_id FROM nested_category WHERE name='FLASH'));
Query OK, 0 rows affected (0.02 sec)

mysql> SELECT CONCAT(REPEAT('*', COUNT(1) - 1), node.name) AS node_name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.category_id ORDER BY node.lft;
+-----------------------+
| node_name             |
+-----------------------+
| ELECTRONICS           |
| *TELEVISIONS          |
| **TUBE                |
| **LCD                 |
| **PLASMA              |
| *PORTABLE ELECTRONICS |
| **MP3 PLAYERS         |
| **CD PLAYERS          |
| **2 WAY RADIOS        |
| *BIG SCREEN           |
+-----------------------+
10 rows in set (0.02 sec)

mysql> call delete_node((SELECT category_id FROM nested_category WHERE name='FLASH'));

Query OK, 0 rows affected (0.02 sec)

+-----------------------+

| node_name |

+-----------------------+

| ELECTRONICS |

| *TELEVISIONS |

| **TUBE |

| **LCD |

| **PLASMA |

| *PORTABLE ELECTRONICS |

| **MP3 PLAYERS |

| **CD PLAYERS |

| **2 WAY RADIOS |

| *BIG SCREEN |

+-----------------------+

10 rows in set (0.02 sec)

四、对预排序树的体会
1、多数查询不需要递归，使用基于整形的比较即可快速处理涉及任意节点祖先或后代的查询；
2、多数查询仅需要访问1-2次数据库，查询计划相对简单；
3、由于lft和rgt为整型且选择性较高，必要时还可以通过对lft和rgt增加索引以提高效率；

参考资料：
1、《Managing Hierarchical Data in MySQL》，原始链接已无法访问，在https://gist.github.com/tmilos/f2f999b5839e2d42d751中有备份；
2、《Joe Celko’s Trees and Hierarchies in SQL for Smarties》，在《Managing Hierarchical Data in MySQL》被强烈推荐；
3、《树形结构的数据库表设计》，https://blog.csdn.net/lj1314ailj/article/details/52074216；

转载时请保留出处，违法转载追究到底：进城务工人员小梅 » MySQL层次关系的存储，预排序树（Modified Preorder Tree）的原理、实现与使用

MySQL层次关系的存储，预排序树（Modified Preorder Tree）的原理、实现与使用

相关推荐

评论抢沙发

相关推荐

评论 抢沙发

评论抢沙发